Kompassrose mit dem GY-271 - Oder, warum man mit dem Handy Achten gehen muss…

Früher war, wenn man mit dem Fahrrad durch eine fremde Gegend radelte, die Kartentasche unumgänglich. Heute hat man ein Handy in der Halterung am Lenker oder, wenn man noch mehr Überblick haben will, ein Tablet im Fahrradkorb. Ich verwende auf meinem Mobilgerät dazu die OsmAnd-App für OpenStreetmap-Karten. Leider hat mein Handy keinen Kompass, so dass man auf den winzigen dynamischen Kompass auf dem OsmAnd-Screen angewiesen ist, der zudem wegfällt, wenn man stehen bleibt, um sich neu zu orientieren. Dazu dreht sich gefühlt dreimal die Karte auf dem Bildschirm, so dass man erst einmal einige 20 m (natürlich in die falsche Richtung) fahren muss, um die Orientierung wiederzuerlangen.

So kam mir die Idee, einen separaten übersichtlichen Kompass mitzuführen, bei dem der Zeiger aka Kompassnadel nicht bei jeder Erschütterung zu tanzen beginnt. Bei der Sichtung älterer Elektor-Hefte verdichtete sich die Idee zu einer elektronischen Lösung, die nun, mindestens eine Elektronik-Generation später, eigentlich noch zuverlässiger und empfindlicher sein müsste.

Bei [1] wurde eine Lösung mit dem Arduino Nano, einem Neopixel-LED-Ring und dem GY-271 vorgestellt, mit Schaltung und Programmcode, was offenbar alles funktionieren sollte und mich zum Kaufen animierte. Da ich gern immer mehrere ICs einer Sorte zur Hand habe, wurden für wenig Geld gleich drei Exemplare des GY-271 im Internet erstanden.

Das Kompassmodul GY-271

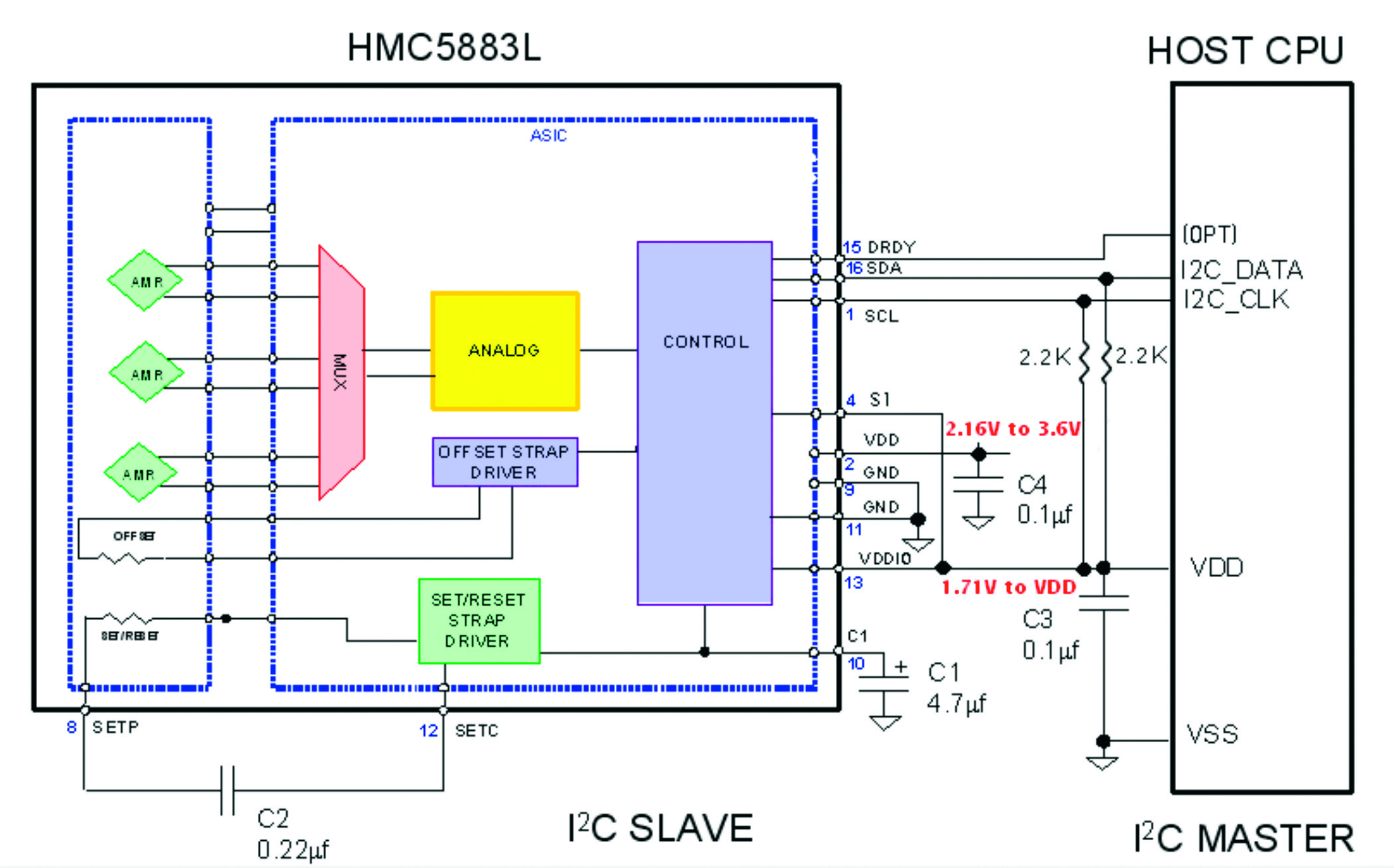
Der GY-271 ist ein für den Arduino geeignetes Breakout-Board, dessen Steckerleiste wunderbar auf ein Steckbrett passt. Das eigentliche IC auf der Platine ist ein 3-Achsen-Kompass-IC mit der Bezeichnung HMC5883L/QMC5883, das offenbar auch in Handys verbaut wird, und daher ein preisgünstiges Massenprodukt ist. Die Innenschaltung des ICs ist in Bild 1 zu sehen. Außer diesem IC sind lediglich ein 3,3-V-LDO-Spannungsregler, einige Puffer- und Bypasskondensatoren sowie zwei Pegelwandler für den I²C-Bus auf der Platine. Daraus können wir folgern, dass das Modul mit 3...5 V versorgt wird und mit einem angeschlossenen Controller (sei es ein Arduino oder ein Raspberry Pi oder sonst ein „intelligenter“ Baustein) über den I²C-Bus kommuniziert. Wie diese Kommunikation vonstatten geht, wird in der beiliegenden detaillierten Dokumentation und in einem kostenlosen, in mehreren Sprachen verfügbaren Anwendungs-E-Book [2] genauestens beschrieben.

Die Verdrahtung des Moduls beschränkt sich auf die – da wir es nirgendwo mit Analogsignalen zu tun haben - unproblematische Stromversorgung. Der LED-Ring wird über die beiden Lötpads für Plus und Masse versorgt. Es gibt nur ein Logik-Signal, das den Takt für das Neopixel bereitstellt. Ansonsten wurde, um Platz zu sparen, ein Arduino Mini Pro verwendet, der nur in der Arduino-IDE entsprechend eingestellt werden muss. Zum Programmieren ist ein FTDI-USB-Seriell-Wandler erforderlich.

So weit, so schlecht

Eigentlich sprach dies alles für einen problemlosen Aufbau und Einsatz des Kompasses an meinem Bike. Doch schon der erste Einsatz war ernüchternd! Es funktionierte eigentlich nur ein Quadrant, dann gab es es einen Sprung der „Nadel“ um 180 Grad. Eine Durchforstung des (mittlerweile zurückgezogenen) Programmlistings auf mögliche Ursachen verlief ergebnislos, ein Fehler war nicht zu finden. Eine Internet-Recherche förderte weitere unzufriedene Stimmen zu Tage, aber der Fehler wurde auf die nicht vorhandene Qualität von Noname-Produkten bei ebay geschoben.

Kurz und gut, als Praktiker musste ich empirisch vorgehen, um dem Fehler auf den Grund zu gehen. Schon in ersten Versuchen konnte ich feststellen, dass eine starke Abhängigkeit von Fremdfeldern gegeben ist, die zum Beispiel in der Nähe meines Laptops auftreten. Von einem allzu kippeligen Versuchsaufbau ist aufgrund der sperrigen Drähte abzuraten, so dass ich einen soliden Versuchsaufbau für die Messungen schuf, wie er in Bild 2 zu sehen ist. Damit Sie erkennen, was Sie dort sehen: Als stabile Basis für den Kompass wurde eine umgedrehte, magnetisch garantiert unverdächtige Kaffeetasse gewählt. Auf dem Tassenboden ist mit Gummis die Platine mit dem (hier unsichtbaren) Sensor und dem Ring der LEDs sowie darunter ein Schreibstift als „Nordweiser“ befestigt, wobei ein Hölzchen und ein Schwämmchen als Abstandshalter und Widerlager gleichzeitig dienen. Auf der Bestückungsseite des GY-271 ist die x- und die y- Richtung angegeben. Die rote Spitze des Stiftes entspricht der Richtung der LED 0 des Rings und der Minus-(!)-x-Richtung des Sensors, der mit der Bestückungsseite nach unten fixiert wurde. Die z-Werte sollen hier nicht betrachtet werden, aber sie sollten möglichst auf Null gehalten werden, um „Unruhe“ im System zu vermeiden. Eventuell lassen sich die z-Werte später mit ein wenig Mathematik nutzen, um Hors-Catégorie-Steigungen im Gebirge zu messen. Die Tasse steht auf einem Blatt Papier, auf dem eine rudimentäre Windrose gezeichnet und dessen Mittelkreis ausgeschnitten ist, damit er sich mitdrehen kann. Und auch wenn er vielleicht nicht so aussieht, hat dieser Aufbau nicht nur zu reproduzierbaren Messergebnissen, sondern auch zu einem bemerkenswerten Aha-Effekt geführt.

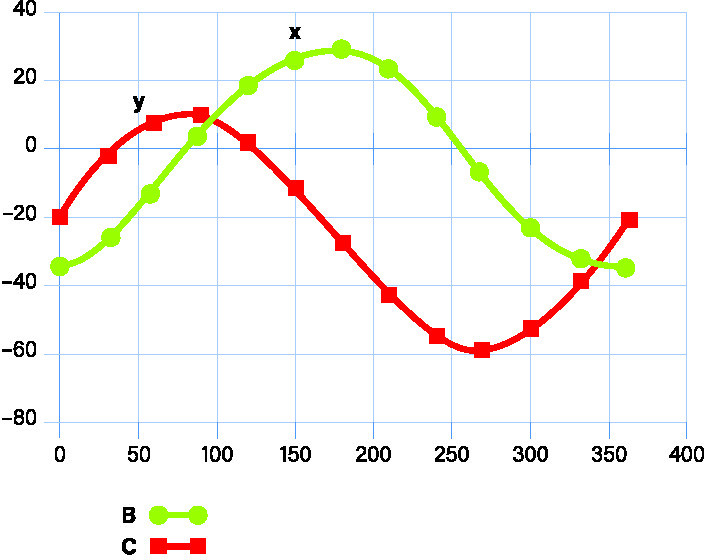
Ich habe den Kaffeetassen-Kompass also gedreht, dabei die x- und y-Werte aufgezeichnet und in dem Excel-Sheet in Bild 3 eingetragen (x-Werte blau, y-Werte rot). Vergleicht man dies mit den idealen Kurven Bild 4, erkennt man sofort das Malheur: Man sieht eine Sinus- und eine Cosinus-Kurve (ein um 90° verschobener Sinus).

In der Schule haben wir gelernt, dass in einem rechtwinkligen Dreieck der Sinus das Verhältnis von Gegenkathete zur Hypotenuse, beim Cosinus von Ankathete zur Hypothenuse und beim Tangens von Gegenkathete zur Ankathete ist. Was einem dazu spontan einfällt: Der Quotient von Sinus zu Cosinus ist der Tangens, weil die Hypotenuse sich ja wegkürzt. Um den Winkel aus den Seiten zu bestimmen, benötigen wir die Umkehrfunktion, den Arkustangens oder arctan.

Arduino kennt den Befehl arctan2, bei dem beide Werte x und y verwendet werden. Eine Normierung auf 1 ist nicht erforderlich, aber die Amplituden sollten gleich sein. Die Nullpunkt-Verschiebung ist als Ursache des Fehlers anzusehen. Nun wird auch klar, warum man mit dem Handy mysteriöse 8-förmige Bewegungen ausführen soll, um eine hohe Genauigkeit der Kompassmessung zu erreichen. Offenbar sind dort HMC-Kompasssensoren eingebaut! Bei einigen Bekannten funktioniert diese Vorgehens- (oder sollte man sagen: Achtgehens-)weise trotzdem nicht, weil die Verschiebung offenbar zu groß war.

Ähnlich könnte ein Verfahren zum „automatischen“ Abgleich beim Arduino erfolgen, bei dem die Maximalwerte erfasst und Korrekturwerte zugefügt werden. Hierzu wäre aber ein Umschalter erforderlich, was den schaltungstechnischen Aufwand von ein auf zwei Pins glatt verdoppeln würde. Da ich aber die komplette Kurve aufgenommen hatte, kannte ich den Grad der Verschiebung und brauchte diesen Wert nur im Programm zu korrigieren.

Ein neues Programm

Großes Plus der ursprünglichen Software war, dass auf die Initialisierung und Signalauswertung des HMC aufgebaut werden konnte. Ich habe einige Änderungen im Monitorprogramm durchgeführt, die riesigen Werte durch 100 dividiert und übersichtlicher angeordnet, denn schließlich kennt der Neopixel-Ring nur zwölf Stellungen, so dass eine Genauigkeit von nur etwa +/-10% ausreichend ist. Wenn man einen größeren Neopixel-Ring oder gar ein graphisches Display verwenden möchte, muss man die großen Werte entsprechend anpassen beziehungsweise verfeinern. Die Ansteuerung des Neopixels habe ich auf der Basis der sehr übersichtlichen Programme von [3] ebenfalls abgespeckt, was sich bei zwölf LEDs als praktikabel herausgestellt hat. Die eigentliche Änderung zur Korrektur des HMC-Fehlers ist in dem Ausschnitt des Source-Codes in Listing 1 zu sehen. Das vollständige und vollständig modifizierte Arduino-Programm kann von [4] heruntergeladen werden. Besonders anschaulich in diesem Sketch ist die Monitor-Funktion, die zu eigenen Experimenten einlädt.

Listing 1: Hartcodierte Kalibrierung der Messungen.

Bewährung in der Praxis

Der Kompass sollte in ein durchsichtiges Kunststoff-Gehäuse eingebaut und am Fahrrad-Lenker befestigt werden. Dabei wurde der freie Aufbau beibehalten, die einzelnen Ebenen durch Plastik-Scheiben getrennt und unten durch eine Platte mit Klebestreifen abgeschlossen. Mit einer weiteren, innen kreisförmig ausgesparten und „gezackten“ Platte wurde der Neopixel-Ring fixiert.

Die Werte wurden mit LED 0 in Richtung Norden aufgenommen, bei den ersten Tests mit der Software stellte sich heraus, dass der LED-Ring aber die Südrichtung anzeigte. Jede Ambition zur Software-Änderung wurde abgewürgt und das Problem pragmatisch gelöst, indem der Kompass mit der LED 6 Richtung Norden fixiert und das Ganze dann in Fahrrad-Längsrichtung montiert wurde. Wenn das Fahrrad in Richtung Norden gedreht wird, leuchtet die vorderste LED. Dreht man das Fahrrad dann nach rechts, leuchtet eine LED weiter links, also weiter Richtung Norden. Genau so ist es auch beabsichtigt!

Allerdings hat mir das Eisenmaterial des Lenkers mit seinem Restmagnetismus einen Strich durch die Rechnung gemacht. Indirekt habe ich aber den Nachweis erbracht, dass der Rahmen tatsächlich aus Aluminium besteht, was durch seine dielektrischen Eigenschaften beim Kompass nicht stört. Da die Schaltung klein ist, wurde sie im Blickfeld am Rahmen fixiert (Bild 5). Beim ersten Praxistest „im Feld“ konnte eine einwandfreie Funktion nachgewiesen werden. Eine Abweichung gab es nur bei einer Eisenbahnbrücke, wahrscheinlich verursacht durch das Feld des Fahrdrahts. Beim nächsten Mal an selber Stelle war keine Abweichung zu erkennen. Insgesamt kann ich mich durch den Kompass im unbekannten Gelände nun viel besser orientieren!

Haben Sie Fragen oder Kommentare?

Haben Sie technische Fragen oder Kommentare zu diesem Artikel? Schreiben Sie uns unter redaktion@elektor.de!