Messung der gesamten harmonischen Verzerrung: Berechnung des Klirrfaktors

Der Klirrfaktor (THD) ist ein wichtiges Maß für den Oberwellengehalt von Signalen in Stromversorgungsnetzen und elektronischen Geräten, wie z. B. Audioverstärkern. Wenn Sie über ein digitales Oszilloskop mit FFT-Funktionalität verfügen, ist die Berechnung des Klirrfaktors nicht allzu schwierig.

Zunächst etwas Terminologie: Harmonischen beschreiben sowohl die Grundfrequenz als auch die Oberwellen eines Signals durch ihre Ordnungszahlen. Oberwellen (overtones) sind alle Signale mit ganzzahligen Vielfachen der Grundfrequenz, beginnend mit der doppelten Frequenz der Grundwelle. Die erste Harmonische entspricht der Grundwelle, die zweite Harmonische entspricht der ersten Oberwelle.

Es gibt zwei wichtige Vertreter der THD-Familie, THDR und THDF. Für beide gilt das Folgende: Je kleiner der Klirrfaktor ist, desto geringer ist der Oberwellengehalt des gemessenen Signals. Je größer der Oberwellengehalt, desto größer der Klirrfaktor. Da Oberwellen in der Regel als Folge von Verzerrungen auftreten, handelt es sich im Grunde um ein Maß für die Quantifizierung nicht linearer Verzerrungen.

In diesem Artikel wird der Begriff "Oberwellen“ verwendet, wenn Vielfache der Grundfrequenz in ihrer Gesamtheit gemeint sind. Der Begriff "Harmonischen" wird verwendet, wenn entweder die Gesamtheit aller Frequenzkomponenten (einschließlich der Grundwelle) oder ein bestimmtes Vielfaches der Grundfrequenz, gekennzeichnet durch eine Ordnungszahl, gemeint ist. Beispiel: 3. Harmonische = 3-mal die Frequenz der Grundwelle.

THDF bezeichnet das Verhältnis aller Oberwellen zur Grundwelle. Diese Größe wird z. B. bei der Messung von Harmonischen in Stromnetzen verwendet. THDR hingegen bezeichnet das Verhältnis aller Oberwellenanteile zum Gesamtsignal. Diese Größe ist besonders in der Audiotechnik beliebt und wird auch als "Klirrfaktor" bezeichnet.

Die Unterscheidung zwischen den beiden Messgrößen ist sehr wichtig, da THDF und THDR zwar eng miteinander verwandt sind, aber unterschiedliche Ergebnisse liefern. In der Literatur und in Datenblättern werden die beiden Werte oft miteinander verwechselt. An manchen Stellen findet man nur den Begriff "THD" ohne weitere Definition der verwendeten Methode, z. B. im Datenblatt von Texas Instruments für den LM386.

In der Praxis lässt sich der THDF relativ einfach aus der Summe der Pegeldifferenzen aller Oberwellen gegenüber der Grundwelle berechnen. Daraus wiederum lässt sich der THDR berechnen.

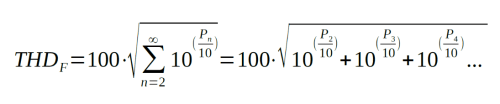
Formel 1: THDF (in %), n = Ordnungszahl der Harmonischen, P = Leistungspegel-Differenz zur Grundwelle in dBc.

Die Formel, die dieses Prinzip beschreibt, mag auf den ersten Blick abschreckend wirken. Vereinfacht ausgedrückt ist THDF die Quadratwurzel aus der Summe aller Spannungsverhältnisse, die sich aus den relativen Pegeldifferenzen einer unendlichen Anzahl von Oberwellen gegenüber der Grundwelle ergeben. Auf den ersten Blick mag dieser Satz ebenso abschreckend wirken wie die Formel selbst. Die Sache ist jedoch nicht so komplex, wie sie scheint.

Der so berechnete THDF -Wert kann dann mit der folgenden Formel in den Klirrfaktor umgerechnet werden:

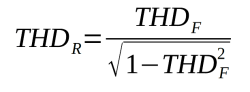
Formel 2: THDR (in %), THDF (in %).

Der Unterschied zwischen THDF und THDR nimmt ab, je kleiner die Werte selbst sind. Unter 1 % ist der Unterschied fast vernachlässigbar.
In Stromversorgungsnetzen wird aus naheliegenden Gründen die Netzfrequenz, z. B. 50 Hz, als Grundfrequenz für die Berechnung des Klirrfaktors verwendet. In der Audiotechnik ist 1 kHz ein gängiger Standard. Praktisch können natürlich nicht unendlich viele Oberschwingungen berücksichtigt werden. In Stromnetzen werden zum Beispiel maximal 50 Oberwellen berücksichtigt. In der Audiotechnik ist es sinnvoll, die nicht hörbaren Oberwellen zu vernachlässigen.

Praktisches Beispiel

Um zu zeigen, dass die langweilige mathematische Theorie in der Praxis gar nicht so schwierig ist, betrachten wir das folgende Beispiel: Ein Sinussignal mit einer Frequenz von 1 kHz wird in den Eingang eines Verstärkers (LM386N-1) eingespeist (Bild 1). Das Ausgangssignal des Verstärkers wird an einen 10 Ω-Widerstand angeschlossen (der als grober Ersatz für die Impedanz eines Lautsprechers dient) und über einen 1:10-Tastkopf an ein Siglent SDS2104X HD-Oszilloskop geleitet (Bild 2).

Im Zeitbereich betrachtet, sieht das Ausgangssignal zunächst recht sauber und sinusförmig aus (Bild 3). Dieser erste Eindruck trügt jedoch, wie ein Blick auf das FFT-Spektrum deutlich zeigt: Neben der Grundschwingung bei 1 kHz sind die harmonischen Komponenten - hier auszugsweise bis 7 kHz - deutlich sichtbar (Bild 4)

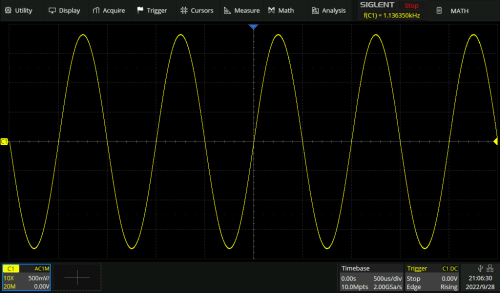
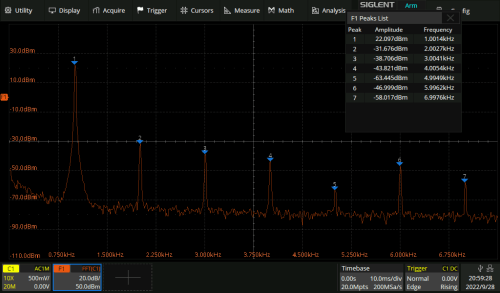
Aus Gründen der Übersichtlichkeit verwarf ich meine ursprüngliche Idee, die Anzahl der betrachteten Oberwellen bis ins Unendliche zu steigern, zumindest bis zur Bandbreitengrenze des Oszilloskops. Ich habe schließlich die Leistungspegel der ersten sieben Harmonischen aufgezeichnet, die dem Leistungspegel der Grundwelle und der ersten sechs Oberwellen entsprechen.

Die meisten Oszilloskope bieten die Möglichkeit, die gemessenen Leistungspegel automatisch in einer praktischen Tabelle anzuzeigen. Die Leistungspegel werden in der Regel in der Einheit dBm angezeigt. Dies ist das Zehnfache des dekadischen Logarithmus des Verhältnisses des gemessenen Wertes zu einer Bezugsgröße. Im Falle von dBm ist die Bezugsgröße 1 mW.

Bevor Berechnungen durchgeführt werden können, müssen die absoluten Leistungspegel in eine Signalpegeldifferenz relativ zur Grundwelle umgerechnet werden. Dabei wird die Einheit dBc (dB relativ zum Träger) verwendet. Zur Umrechnung muss der Leistungspegel der Grundwelle von den Leistungspegeln aller Oberwellen subtrahiert werden. Zum Beispiel für die 2. Harmonische (= 1. Oberwelle): -31,7 dBm - 22,1 dBm = -53,8 dBc.

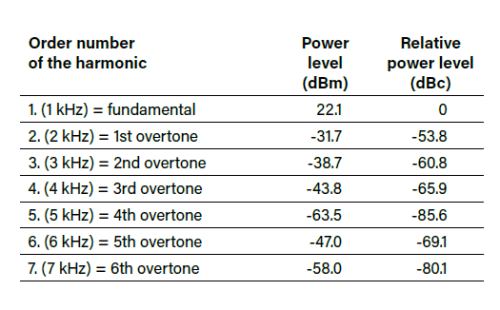
In Tabelle 1 sind die Harmonischen mit ihren Ordnungszahlen, den absoluten Leistungspegeln in dBm (gerundet) und den berechneten Leistungspegeldifferenzen relativ zur 1. Harmonische zusammengefasst. Die relativen Leistungspegel aus Tabelle 1 können direkt in Formel 1 eingesetzt werden.

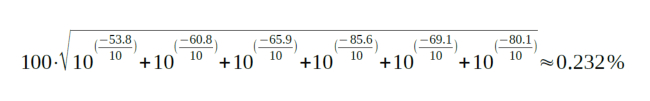
Der THDF Wert des Verstärkers (bis 7 kHz betrachtet) beträgt somit etwa 0,232 %. Mit der zweiten Formel kann dann auch THDR (der Klirrfaktor) berechnet werden.

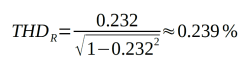
Der Klirrfaktor beträgt somit etwa 0,239 %. Im Datenblatt des LM386 ist ein Klirrfaktor von 0,2 % angegeben. Das kommt den hier berechneten Werten recht nahe. Leider gibt Texas Instruments weder den im Datenblatt angegebenen THD-Typ noch die Anzahl der in die Messung eingeflossenen Oberwellen an.

Beschränkungen und Hinweise

Die hier vorgestellte Methode findet ihre Grenzen im Dynamikbereich des Analog-Digital-Wandlers (ADC) des verwendeten Oszilloskops. In der Regel handelt es sich um 8-Bit-ADCs mit einem theoretischen Dynamikbereich von etwa 48 dB. Diese können bis zu einem minimalen Klirrfaktor von etwa 3 % verwendet werden.

Aufmerksamen Lesern wird aufgefallen sein, dass der oben als Beispiel berechnete Klirrfaktor deutlich unter dieser Grenze liegt. Dies ist möglich, weil ich ein 12-Bit-Oszilloskop verwendet habe. Bei 12-Bit-Oszilloskopen liegt der theoretische Dynamikbereich bei etwa 72 dB. Das bedeutet, dass THD-Werte ab etwa 0,2 % im Bereich des Möglichen liegen. Um diese Grenzen bestmöglich auszunutzen, ist jedoch Vorsicht geboten: Der tatsächlich verfügbare Dynamikbereich hängt auch stark von der vertikalen Auslenkung ab! Wird der ADC zu stark ausgelenkt, kommt es zu Verzerrungen, wird er zu wenig ausgelenkt, geht wertvoller Dynamikbereich verloren.

Wenn Sie diese Methode direkt ausprobieren wollen, fragen Sie sich vielleicht, woher Sie Referenzsignale mit bekannten THD-Werten bekommen. Ein einfacher Signalgenerator kann hier helfen: Ein einigermaßen symmetrisches Rechtecksignal mit einem Tastverhältnis von 50 % hat einen Klirrfaktor von etwa 48,3 %. Bei einem ebenso symmetrischen Dreieckssignal mit demselben Tastverhältnis liegt der THDF immer noch bei 12,1 %. Wenn Sie etwas tiefer in die Materie einsteigen und auch die Herleitung der Formeln verstehen wollen, finden Sie weitere Informationen unter https://baltic-lab.com/thd/ und http://dx.doi.org/10.5281/zenodo.6969825.

220398-01 - Dieser Artikel erschien zuerst in Elektor Mag Jan/Feb 2023. 

Fragen oder Kommentare zum Klirrfaktor?

Haben Sie technische Fragen oder Kommentare zum Klirrfaktor (THD) oder zu einem der anderen in diesem Artikel behandelten Themen? Schicken Sie eine E-Mail an den Autor mailto autor oder kontakt Elektor.