Die wichtigsten Formeln für jeden Elektroniker
28. Juli 2020
über
über
Will man den Wert eines Widerstands berechnen, benötigt man dafür die richtigen Formeln. Es ist wichtig, die diversen Gesetze rund um das Thema Strom im Auge zu behalten, die unserem faszinierenden Thema Elektronik zugrunde liegen. Versucht man ein Gerät zu reparieren oder will man verstehen, warum ein Schaltkreis nicht funktioniert, kann ein Blick in die Grundlagen aufschlussreich sein und die erforderlichen Erkenntnisse liefern, auf denen man aufbauen kann.
Von fast ebenso großem Interesse sind die Menschen, nach denen die bekannten Formeln und Gesetze benannt wurden. Lange vor dem Internet und der Online-Bestellung von Bauteilen war die Anschaffung von elektrischen Bauteilen für die Forschung eine teure Angelegenheit. Außerdem war der Zugang zu diesen Teilen nur für die Zeitgenossen möglich, die bei diesen großen Gelehrten studiert haben. Es ist erstaunlich, dass ihre harte Arbeit mehr als ein Jahrhundert später immer noch eine wichtige Rolle in unserem Elektronikerleben spielt.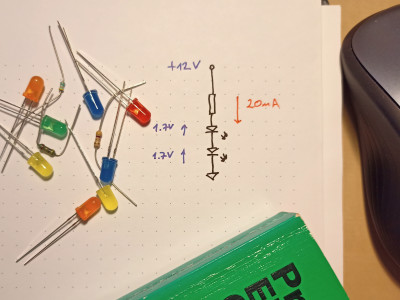 Ein Großteil der frühen Elektrotechnik konzentrierte sich auf die Herausforderungen der noch jungen Telegraphentechnik. Telegrafisten verwendeten in dieser Pionierzeit noch unterschiedliche Einheiten für den elektrischen Widerstand – man denke nur an die Jacobische Widerstandseinheit (Kupferdraht von 7,6 m Lange und 0,67 mm Durchmesser, etwa 0,64 Ω) oder die „Deutsche Meile“ (Eisendraht mit 1/6“ Durchmesser und 7532,5 m Länge, etwa 57,4 Ω). Doch 1861 schlugen zwei britische Ingenieure vor, nicht nur die Spannung in Volt zu messen, sondern auch das Ohm als Einheit für den Widerstand zu etablieren. 12 Jahre später wurde das Ω von der British Assoziation for the Advancement of Science akzeptiert, und 20 Jahre später wurde das auf dem ersten Internationalen Elektrizitätskongress in Paris abgesegnet.
Ein Großteil der frühen Elektrotechnik konzentrierte sich auf die Herausforderungen der noch jungen Telegraphentechnik. Telegrafisten verwendeten in dieser Pionierzeit noch unterschiedliche Einheiten für den elektrischen Widerstand – man denke nur an die Jacobische Widerstandseinheit (Kupferdraht von 7,6 m Lange und 0,67 mm Durchmesser, etwa 0,64 Ω) oder die „Deutsche Meile“ (Eisendraht mit 1/6“ Durchmesser und 7532,5 m Länge, etwa 57,4 Ω). Doch 1861 schlugen zwei britische Ingenieure vor, nicht nur die Spannung in Volt zu messen, sondern auch das Ohm als Einheit für den Widerstand zu etablieren. 12 Jahre später wurde das Ω von der British Assoziation for the Advancement of Science akzeptiert, und 20 Jahre später wurde das auf dem ersten Internationalen Elektrizitätskongress in Paris abgesegnet.
Die Einheit wurde nach dem deutschen Physiker Georg Simon Ohm benannt. Seine Arbeiten im frühen 19. Jahrhundert führten zur bekannten Formel U = I × R, dem bis heute relevanten Ohmschen Gesetz. Man kann diese Formel auf drei verschiedene Arten umstellen, je nachdem, ob man die Spannung den Strom oder der Widerstand berechnen will:
Die erste Anwendung des Ohmschen Gesetzes erfahren angehende Elektroniker bei der Berechnung des Strombegrenzungswiderstands für eine LED. Ein Beispiel: Bei einer Versorgungsspannung von 12 V und zwei in Reihe geschalteten LEDs berechnet man den erforderliche Widerstand wie folgt: Zunächst wird die „Vorwärtsspannung“ der LEDs benötigt. Diese beträgt für rote Standard-LEDs etwa 1,7 V – in unserem Beispiel wird sie zweimal von der Versorgungsspannung subtrahiert:
Wenn der Betriebsstrom der LEDs typische 20 mA beträgt, kann damit nun der erforderliche Widerstand berechnet werden:
Wenn 20 mA durch unseren Widerstand fließen, können wir die an ihm in Wärme umgesetzte Leistung wie folgt bestimmen:
Dies bedeutet, dass man mit einem Widerstand mit einer Belastbarkeit von ¼-W auf der sicheren Seite liegt.
 Die bisher diskutierten Formeln scheinen einfach und leicht zu handhaben, Das liegt aber nur daran, dass sie schon etabliert sind und dass man heute mit standardisierten Einheiten arbeitet. Früher waren die Einheiten ab er eben noch nicht standardisiert es noch keine Standardeinheiten. Arbeiten wie die von Herrn Ohm wurden damals auch abfällig als „Hirngespinst“ bezeichnet. Dieser Art „neuen Denkens“ war oft unvereinbar mit damals etablierten Theorien.
Die bisher diskutierten Formeln scheinen einfach und leicht zu handhaben, Das liegt aber nur daran, dass sie schon etabliert sind und dass man heute mit standardisierten Einheiten arbeitet. Früher waren die Einheiten ab er eben noch nicht standardisiert es noch keine Standardeinheiten. Arbeiten wie die von Herrn Ohm wurden damals auch abfällig als „Hirngespinst“ bezeichnet. Dieser Art „neuen Denkens“ war oft unvereinbar mit damals etablierten Theorien.
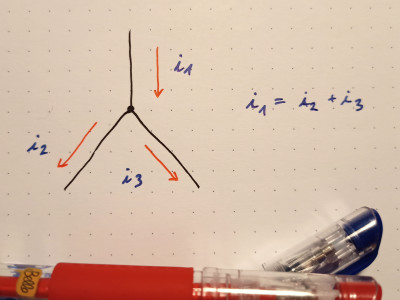
Die Knotenregel bzw. das 1. Kirchhoffsche Gesetz ist längst ebenfalls Standard. Laut ihm ist die algebraische Summe der Ströme an jedem Knoten in einem Stromkreis gleich Null. Wenn man es genau nimmt, ist das der Grund dafür, dass in zwei in Reihe geschalteten LEDs der jeweils gleiche Strom fließt. Betrachtet man die Verbindung zwischen den beiden LEDs als einen Knoten, beträgt der Strom, der von der ersten LED in den Knotenpunkt eintritt, 20 mA. Das ist exakt der Strom, der diesen Knoten wieder verlässt und durch die zweite LED fließt. Folglich muss der durch den Widerstand fließende Strom ebenfalls 20 mA betragen.
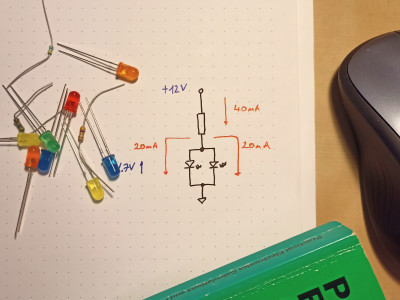 Wenn man die vorherige Schaltung so modifiziert, dass nun die LEDs parallel geschaltet sind, ist der Knotenpunkt interessant, an dem Strom vom Widerstand in die beiden LEDs fließt. Wenn jede LED einen Strom von je 20 mA aus dem Knoten zieht (bei gleicher Vorwärtsspannung und gleichem Innenwiderstand der beiden LEDs). muss durch den Widerstand in den Knoten fließende Strom die Summe = 40 mA sein. Der nötige Widerstandswert lässt sich dann wie folgt berechnen:
Wenn man die vorherige Schaltung so modifiziert, dass nun die LEDs parallel geschaltet sind, ist der Knotenpunkt interessant, an dem Strom vom Widerstand in die beiden LEDs fließt. Wenn jede LED einen Strom von je 20 mA aus dem Knoten zieht (bei gleicher Vorwärtsspannung und gleichem Innenwiderstand der beiden LEDs). muss durch den Widerstand in den Knoten fließende Strom die Summe = 40 mA sein. Der nötige Widerstandswert lässt sich dann wie folgt berechnen:
Da nun ja 40 mA fließen, stellt sich die Frage, ob ein Widerstand mit einer Belastbarkeit von ¼ W noch ausreicht. Dies lässt sich wie zuvor überprüfen:
Die Schaltungsänderung mag zwar klein und nicht praxisgerecht sein (da man LEDs nicht ohne Not parallel schaltet), aber dennoch wird klar, dass in diesem Beispiel ein Widerstand von mindestens ½ W Belastbarkeit ausgesucht werden müsste.
Von fast ebenso großem Interesse sind die Menschen, nach denen die bekannten Formeln und Gesetze benannt wurden. Lange vor dem Internet und der Online-Bestellung von Bauteilen war die Anschaffung von elektrischen Bauteilen für die Forschung eine teure Angelegenheit. Außerdem war der Zugang zu diesen Teilen nur für die Zeitgenossen möglich, die bei diesen großen Gelehrten studiert haben. Es ist erstaunlich, dass ihre harte Arbeit mehr als ein Jahrhundert später immer noch eine wichtige Rolle in unserem Elektronikerleben spielt.
Ohmsches Gesetz
 Ein Großteil der frühen Elektrotechnik konzentrierte sich auf die Herausforderungen der noch jungen Telegraphentechnik. Telegrafisten verwendeten in dieser Pionierzeit noch unterschiedliche Einheiten für den elektrischen Widerstand – man denke nur an die Jacobische Widerstandseinheit (Kupferdraht von 7,6 m Lange und 0,67 mm Durchmesser, etwa 0,64 Ω) oder die „Deutsche Meile“ (Eisendraht mit 1/6“ Durchmesser und 7532,5 m Länge, etwa 57,4 Ω). Doch 1861 schlugen zwei britische Ingenieure vor, nicht nur die Spannung in Volt zu messen, sondern auch das Ohm als Einheit für den Widerstand zu etablieren. 12 Jahre später wurde das Ω von der British Assoziation for the Advancement of Science akzeptiert, und 20 Jahre später wurde das auf dem ersten Internationalen Elektrizitätskongress in Paris abgesegnet.
Ein Großteil der frühen Elektrotechnik konzentrierte sich auf die Herausforderungen der noch jungen Telegraphentechnik. Telegrafisten verwendeten in dieser Pionierzeit noch unterschiedliche Einheiten für den elektrischen Widerstand – man denke nur an die Jacobische Widerstandseinheit (Kupferdraht von 7,6 m Lange und 0,67 mm Durchmesser, etwa 0,64 Ω) oder die „Deutsche Meile“ (Eisendraht mit 1/6“ Durchmesser und 7532,5 m Länge, etwa 57,4 Ω). Doch 1861 schlugen zwei britische Ingenieure vor, nicht nur die Spannung in Volt zu messen, sondern auch das Ohm als Einheit für den Widerstand zu etablieren. 12 Jahre später wurde das Ω von der British Assoziation for the Advancement of Science akzeptiert, und 20 Jahre später wurde das auf dem ersten Internationalen Elektrizitätskongress in Paris abgesegnet.Die Einheit wurde nach dem deutschen Physiker Georg Simon Ohm benannt. Seine Arbeiten im frühen 19. Jahrhundert führten zur bekannten Formel U = I × R, dem bis heute relevanten Ohmschen Gesetz. Man kann diese Formel auf drei verschiedene Arten umstellen, je nachdem, ob man die Spannung den Strom oder der Widerstand berechnen will:
U = I × R, I = U ÷ R und R = U ÷ I
Die erste Anwendung des Ohmschen Gesetzes erfahren angehende Elektroniker bei der Berechnung des Strombegrenzungswiderstands für eine LED. Ein Beispiel: Bei einer Versorgungsspannung von 12 V und zwei in Reihe geschalteten LEDs berechnet man den erforderliche Widerstand wie folgt: Zunächst wird die „Vorwärtsspannung“ der LEDs benötigt. Diese beträgt für rote Standard-LEDs etwa 1,7 V – in unserem Beispiel wird sie zweimal von der Versorgungsspannung subtrahiert:
12 V – 1,7 V – 1,7 = 8,6 V
Wenn der Betriebsstrom der LEDs typische 20 mA beträgt, kann damit nun der erforderliche Widerstand berechnet werden:
R = 8,6 V ÷ 0,02 A = 430 Ω
Elektrische Leistung
Sobald der Widerstandswert definiert ist, sollte man sicherstellen, dass er für die an ihm entstehende thermische Leistung richtig dimensioniert ist. Dies führt direkt zu einer weiteren wichtigen Formel. Es geht um die Leistung (P), gemessen in Watt (W). Sie kann für mit der Formel „P = U x I“ berechnet werden. Man kann die Leistungsformel auch gleich mit dem Ohmschen Gesetz kombinieren, so dass der Widerstand zur Berechnung der Leistung wie folgt verwendet werden kann:P = U × I also P = U2 ÷ R oder P = I2 × R
Wenn 20 mA durch unseren Widerstand fließen, können wir die an ihm in Wärme umgesetzte Leistung wie folgt bestimmen:
P = I2 × R = (0,02 A)2 × 430 Ω = 172 mW
Dies bedeutet, dass man mit einem Widerstand mit einer Belastbarkeit von ¼-W auf der sicheren Seite liegt.
Kirchhoffsche Regeln
 Die bisher diskutierten Formeln scheinen einfach und leicht zu handhaben, Das liegt aber nur daran, dass sie schon etabliert sind und dass man heute mit standardisierten Einheiten arbeitet. Früher waren die Einheiten ab er eben noch nicht standardisiert es noch keine Standardeinheiten. Arbeiten wie die von Herrn Ohm wurden damals auch abfällig als „Hirngespinst“ bezeichnet. Dieser Art „neuen Denkens“ war oft unvereinbar mit damals etablierten Theorien.
Die bisher diskutierten Formeln scheinen einfach und leicht zu handhaben, Das liegt aber nur daran, dass sie schon etabliert sind und dass man heute mit standardisierten Einheiten arbeitet. Früher waren die Einheiten ab er eben noch nicht standardisiert es noch keine Standardeinheiten. Arbeiten wie die von Herrn Ohm wurden damals auch abfällig als „Hirngespinst“ bezeichnet. Dieser Art „neuen Denkens“ war oft unvereinbar mit damals etablierten Theorien.Die Knotenregel bzw. das 1. Kirchhoffsche Gesetz ist längst ebenfalls Standard. Laut ihm ist die algebraische Summe der Ströme an jedem Knoten in einem Stromkreis gleich Null. Wenn man es genau nimmt, ist das der Grund dafür, dass in zwei in Reihe geschalteten LEDs der jeweils gleiche Strom fließt. Betrachtet man die Verbindung zwischen den beiden LEDs als einen Knoten, beträgt der Strom, der von der ersten LED in den Knotenpunkt eintritt, 20 mA. Das ist exakt der Strom, der diesen Knoten wieder verlässt und durch die zweite LED fließt. Folglich muss der durch den Widerstand fließende Strom ebenfalls 20 mA betragen.
 Wenn man die vorherige Schaltung so modifiziert, dass nun die LEDs parallel geschaltet sind, ist der Knotenpunkt interessant, an dem Strom vom Widerstand in die beiden LEDs fließt. Wenn jede LED einen Strom von je 20 mA aus dem Knoten zieht (bei gleicher Vorwärtsspannung und gleichem Innenwiderstand der beiden LEDs). muss durch den Widerstand in den Knoten fließende Strom die Summe = 40 mA sein. Der nötige Widerstandswert lässt sich dann wie folgt berechnen:
Wenn man die vorherige Schaltung so modifiziert, dass nun die LEDs parallel geschaltet sind, ist der Knotenpunkt interessant, an dem Strom vom Widerstand in die beiden LEDs fließt. Wenn jede LED einen Strom von je 20 mA aus dem Knoten zieht (bei gleicher Vorwärtsspannung und gleichem Innenwiderstand der beiden LEDs). muss durch den Widerstand in den Knoten fließende Strom die Summe = 40 mA sein. Der nötige Widerstandswert lässt sich dann wie folgt berechnen:12 V – 1,7 = 10,3 V
R = U ÷ I = 10,3 V ÷ 0,04 A= 257,5 Ω
R = U ÷ I = 10,3 V ÷ 0,04 A= 257,5 Ω
Da nun ja 40 mA fließen, stellt sich die Frage, ob ein Widerstand mit einer Belastbarkeit von ¼ W noch ausreicht. Dies lässt sich wie zuvor überprüfen:
P = I2 x R = (0,04 A)2 × 257,5 Ω = 412 mW
Die Schaltungsänderung mag zwar klein und nicht praxisgerecht sein (da man LEDs nicht ohne Not parallel schaltet), aber dennoch wird klar, dass in diesem Beispiel ein Widerstand von mindestens ½ W Belastbarkeit ausgesucht werden müsste.
Formeln helfen
Wenn Sie also nicht sicher sind, ob die Bauteilewerte in einer Schaltung passen, riskieren Sie einen Blick zurück zu den Grundlagen! Die Arbeit der Physiker des 19. Jahrhunderte ist heute genauso relevant wie damals. Wenn Ihre Schaltung einmal nicht wie erwartet funktionieren sollte, nehmen Sie sich die Zeit, um Ihre praktische Realität mit der Theorie abzugleichen. Diese unumgänglichen Formeln und Gesetze können nämlich erklären, warum Ströme oder Spannungen auf Ihrem Steckbrett nicht mit Ihren Erwartungen übereinstimmen.Mehr anzeigen
Weniger anzeigen


Diskussion (7 Kommentare)